※本セミナはZoomを使ったオンライン同時開催セミナです.
オンライン受講を希望される場合は,セミナ申込後,メールでご連絡ください.
詳細は,オンライン同時開催セミナについてをお読みください.
本セミナでは,特に抵抗器,コンデンサ,コイルから構成される電気回路の働きを学ぶ上で必要になるフーリエ変換(注),ラプラス変換を学びたい方と,これらをアナログ電気回路解析に応用したいと考えている方を対象として想定している.
ところで,フーリエ変換,ラプラス変換は電気回路の解析だけではなく,それ以外の広い分野で役に立っているが,このセミナでは電気回路を扱う上での応用に的を絞ってフーリエ変換,ラプラス変換とこれらを使った電気回路の解析法について解説を行っていく.
なお,取り扱うテーマの性格上,数式が多くなるのは避けられないが,できるだけイメージと結びつくように,いろいろなデモ・プログラムも使いながら,説明を行っていく.デモ・プログラムでは,波形や周波数特性が,回路素子の値を変えるとどのように変化するのかを見るだけでなく,それを音として耳で聴いて確認するようなことも行なっていく.
なお,逆ラプラス変換のFFTを使う数値計算法の解説はあまり見かけないが,その方法についても取り上げる.
デモ・プログラムはC# で作成したものを使うが,セミナ受講者には実行可能ファイルだけではなく,作成した際のプロジェクトに含まれる,ソース・プログラムを含むファイル一式も提供する.
----------------------------
(注)「フーリエ級数展開」は「フーリエ変換」の特別な場合であるため,ここで使っている「フーリエ変換」という用語には「フーリエ級数展開」も含まれる.
※ 講師作成のプログラムはお持ち帰り可能です.
1.フーリエ級数を使う電気回路解析の第1歩
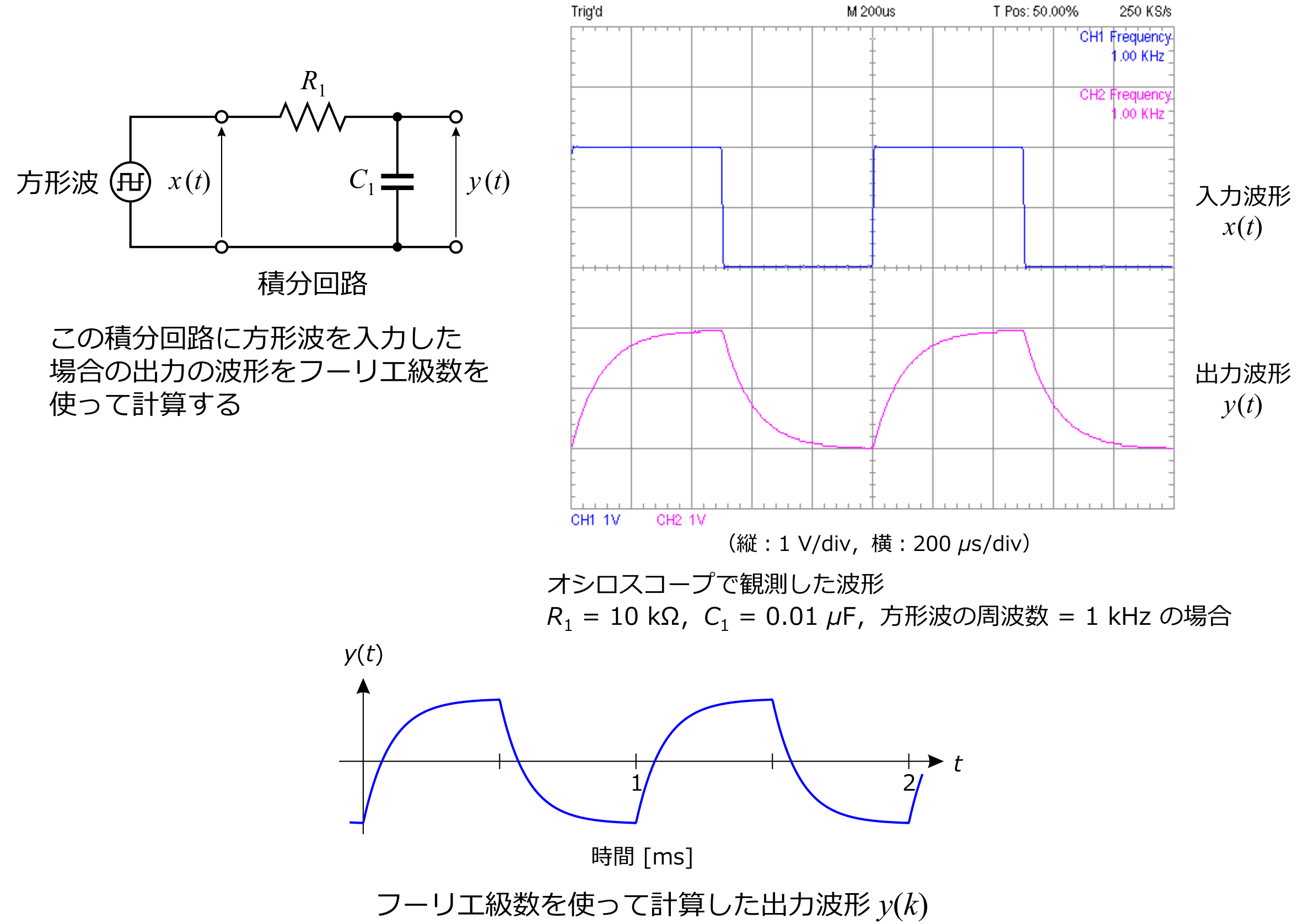
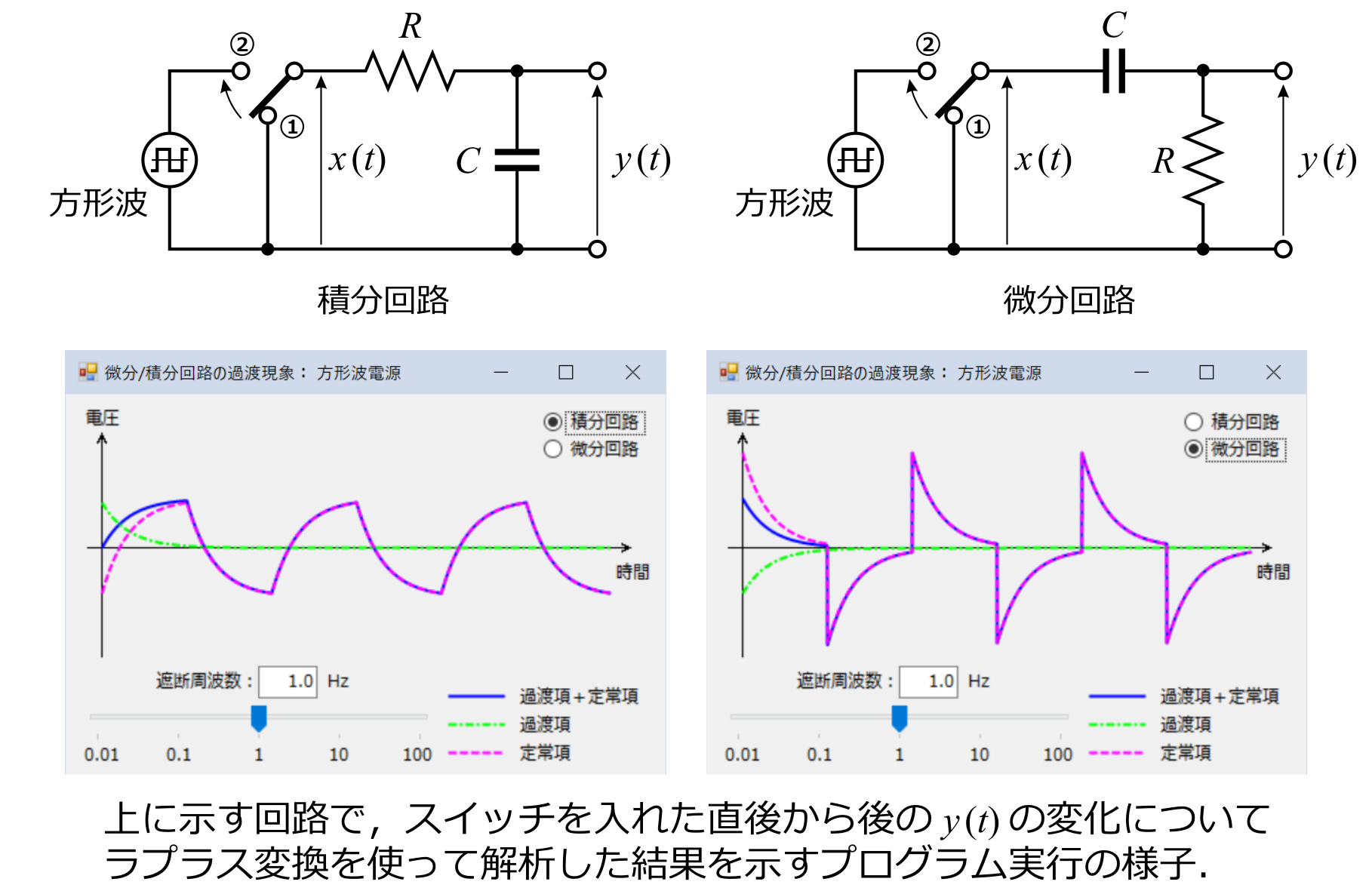
1.1 方形波を簡単な電気回路に入力したときの出力波形を求める
1.2 方形波のフーリエ級数展開とその意味
1.3 フーリエ級数を使って出力波形を求める方法の考え方
2.フーリエ級数展開とフーリエ変換
2.1 フーリエ係数の求め方
2.2 周期信号のフーリエ級数展開の例
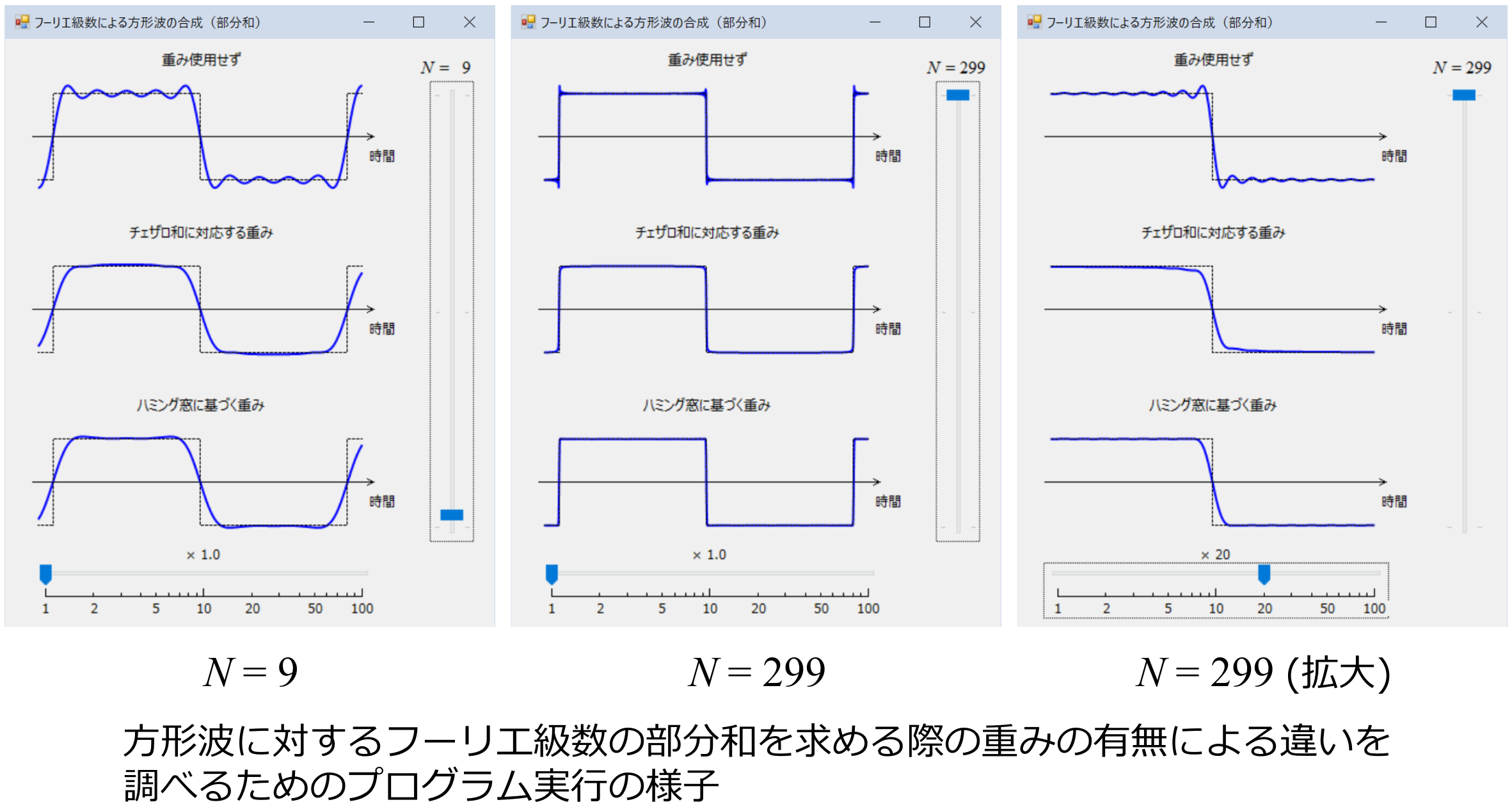
2.3 フーリエ級数の部分和とギブスの現象
2.4 複素形式のフーリエ級数展開
2.5 フーリエ変換と複素フーリエ級数
2.6 フーリエ変換の例
3.周波数応答とフーリエ変換および周波数応答の応用
3.1 周波数応答を求めるための準備
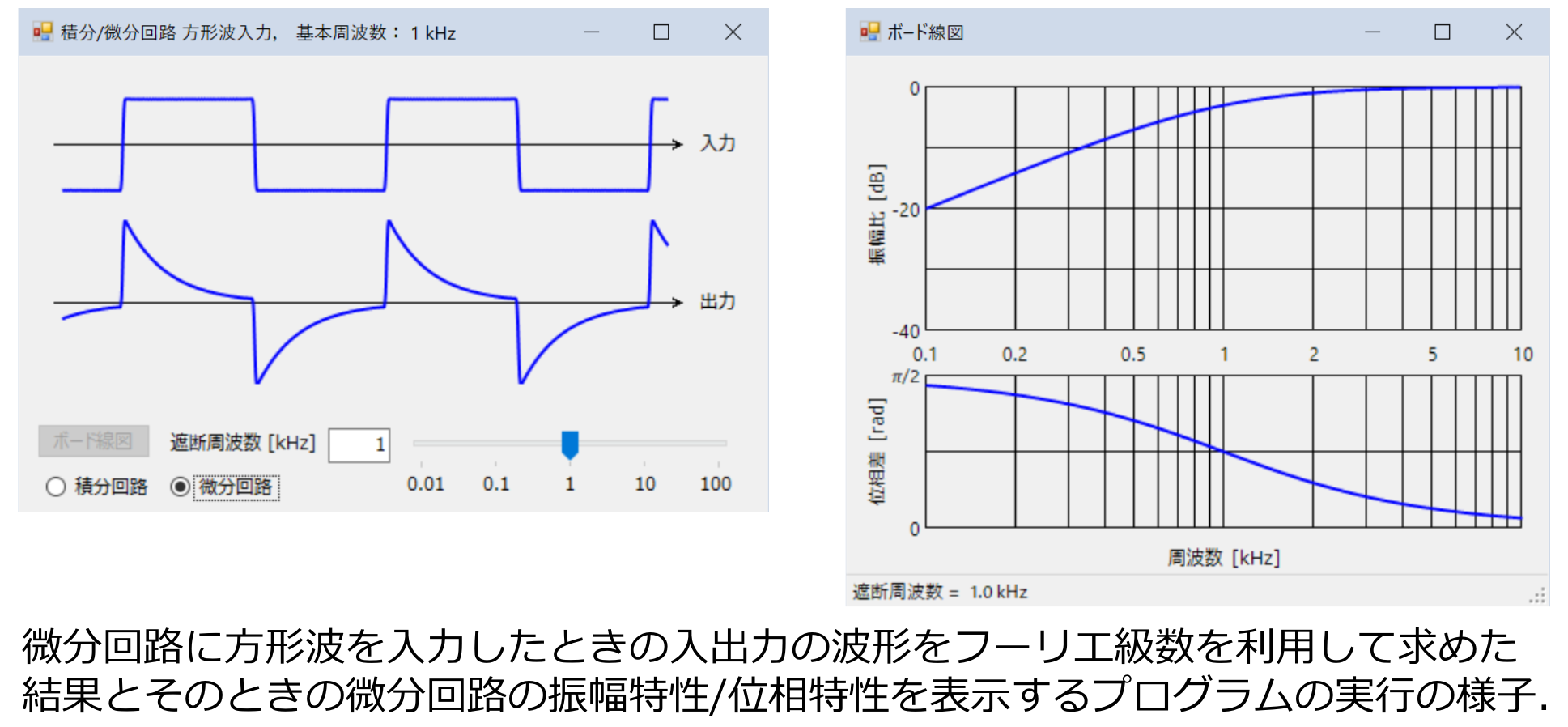
3.2 電気回路素子とフーリエ変換および周波数応答
3.3 周波数応答とフーリエ級数を使う回路解析
3.4 複雑な電気回路の周波数応答の計算法 - 4端子回路の接続を使う方法
3.5 周波数応答とフーリエ級数を使う回路解析の一般化
4.ラプラス変換の第1歩
4.1 電気回路の過渡現象とラプラス変換
4.2 ラプラス変換の計算方法
4.3 逆ラプラス変換の計算方法
4.4 電気回路とラプラス変換
4.5 伝達関数
5.ラプラス変換による電気回路の過渡現象解析
5.1 信号源が直流の場合
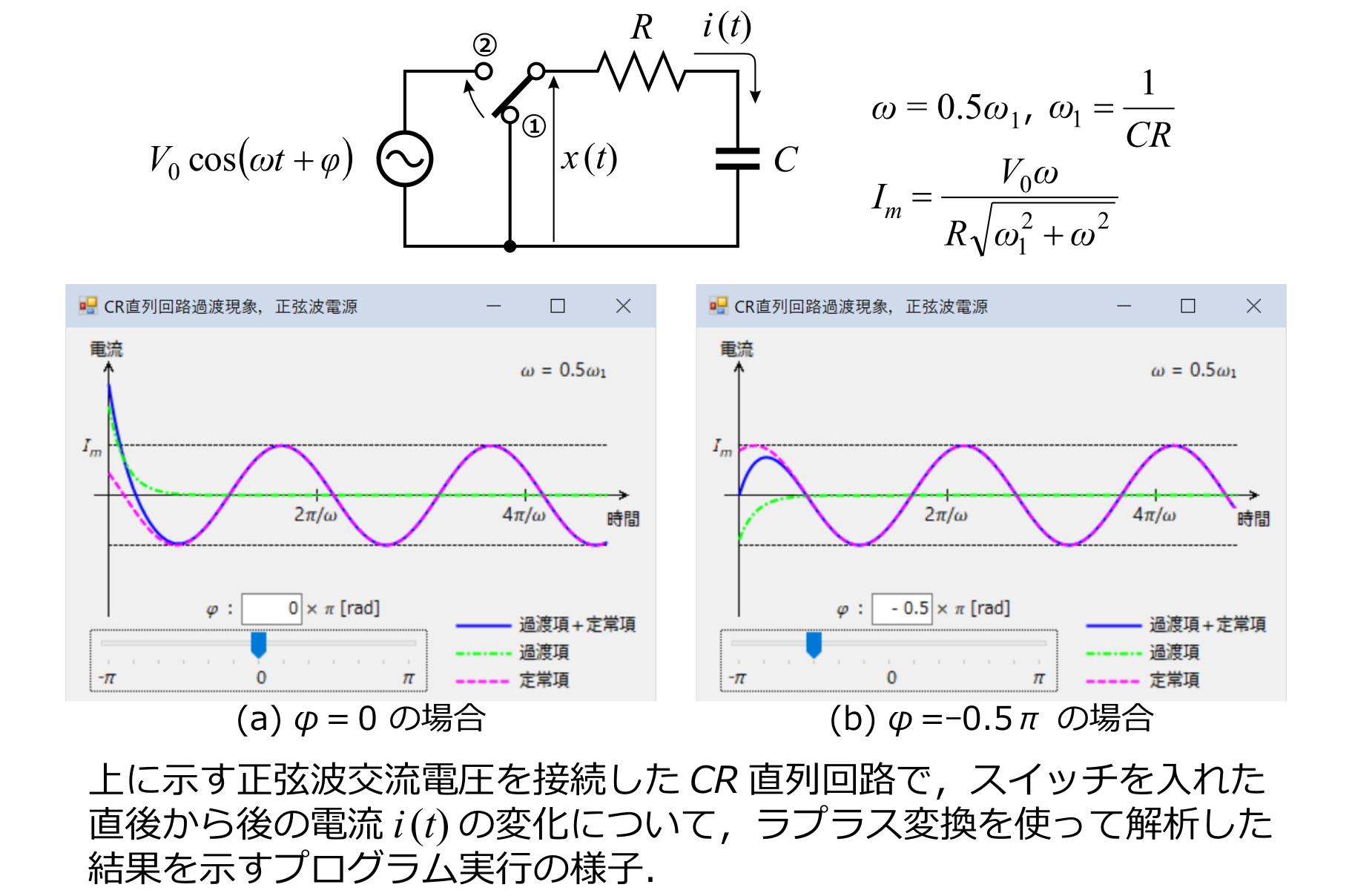
5.2 信号源が周期波形の場合-その1:正弦波
5.3 信号源が周期波形の場合-その2:非正弦波
5.4 逆ラプラス変換のFFTを使う数値計算法
 ●対象聴講者
●対象聴講者
・電気回路解析で必要になるフーリエ変換/ラプラス変換を学びたい方
・電気回路解析においてフーリエ変換/ラプラス変換の使い分けについて理解したい方
・フーリエ変換/ラプラス変換を利用して電気回路の電流や電圧の波形やそのスペクトルを求めたい方
・高校で行う程度の微分/積分,複素数の話を聞いたことのある方が望ましい.
●講演の目標
・フーリエ変換/ラプラス変換に関する計算ができるようになる
・フーリエ変換を使って,定常状態の電気回路解析ができるようになる
・ラプラス変換を使って,過渡状態の電気回路解析ができるようになる